EXINT is a byte-aligned universal code with complete support for the integers. It is byte-order agnostic and has O(1) time performance when bounded by the system datapath, integer, or memory width.
The byte is taken to have the standard width of 8 bits.
In this context, byte-alignment is intended to mean that the unit of composition is the byte. This is explicitly stated due to the fact that not all universal codes for the integers are byte-aligned.
The EXINT structure has a byte-aligned prefix and suffix. Together these specify a uniquely decodable codeword for any integer. This gives it the prefix-free property.
The prefix portion is a byte sequence encoding an integer partition representing a sum for the length in bytes of the suffix. Each byte represents one of the terms of the sum and must be on the interval [0, 254]. If the prefix is zero then the suffix must be omitted.
Except for byte-alignment, no restrictions are placed on the structure of the suffix. This enables the encapsulation of arbitrary data, including the potential for recursive EXINT encoding. As a consequence, an integer representation may be of any byte-ordering or representation.
The attached C implementation of EXINT is approximately 1.7 cycles per byte.
As a result of the encapsulation of the suffix structure, the algorithm can be made O(1) time by bounding the maximum suffix length to that of the native integer width of the system.
Conventional universal codes such as Levenstein coding [1], Elias delta coding [2], and Fibonacci coding [3] must be padded and aligned when used on byte-addressible systems. This causes an average inflation on their storage requirements and processing time. The following graph has made such adjustments for a normalized comparison with EXINT.
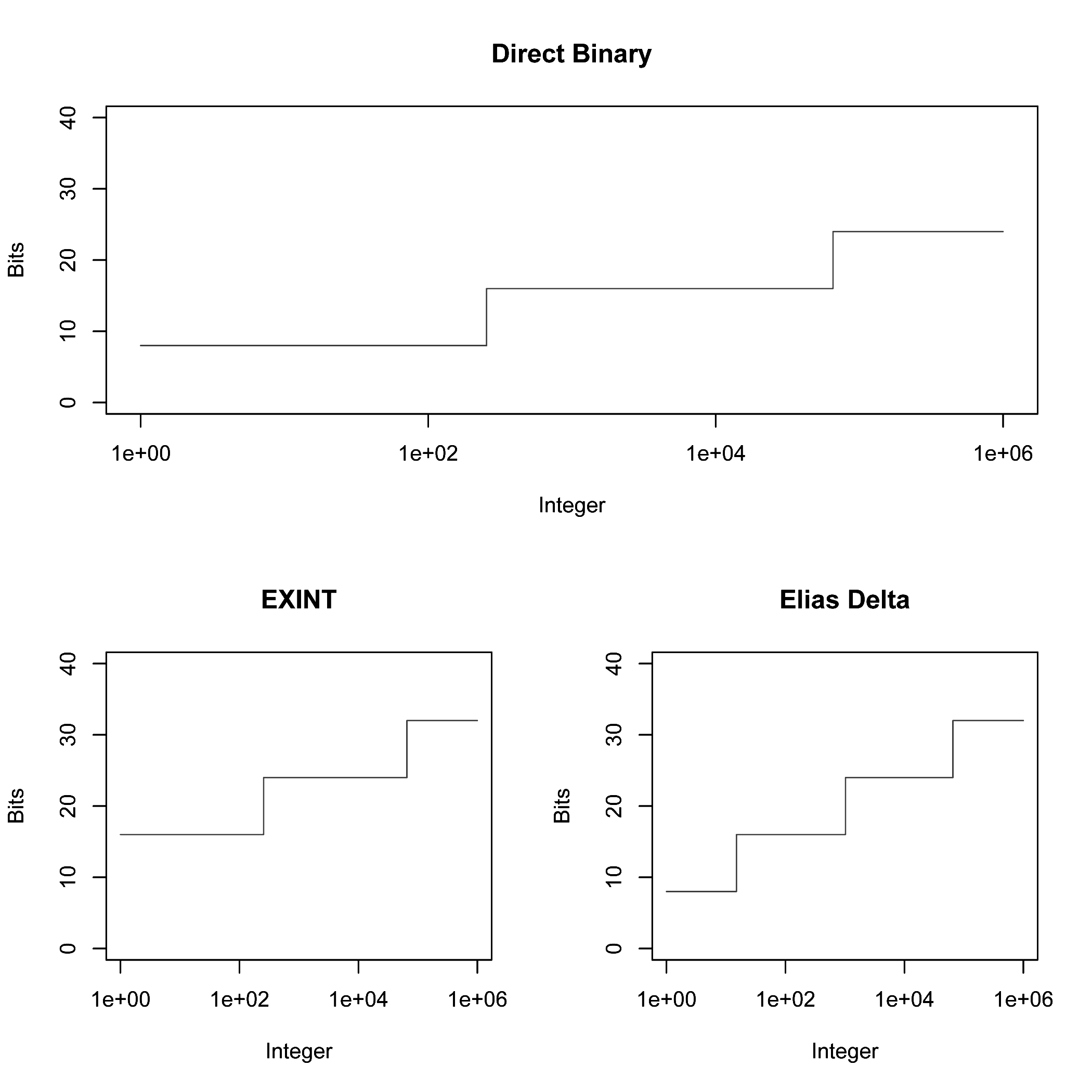
EXINT eliminates the overhead associated with bit-aligned universal codes for the integers while retaining their unique properties. Further, as indicated by the graph, EXINT is comparable in storage requirements to Elias delta coding.
The following formula can be used to calculate the number of bytes required to represent an EXINT sequence for some integer x:
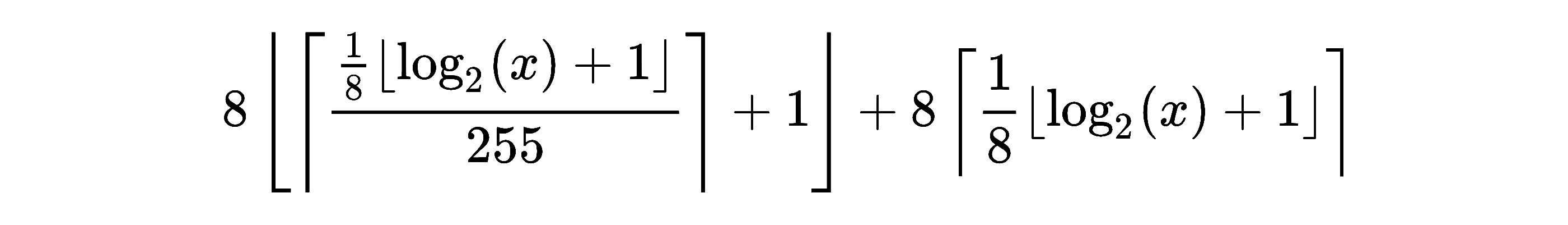
The following is an ANSI C implementation of EXINT for 64-bit unsigned integers.
Download SourceLevenshtein, V. I. (1968). On the redundancy and delay of decodable coding of natural numbers. Translation from Problems in Cybernetics Nauka Moscow, 20, 173–179.
Elias, P. (1975). Universal Codeword Sets and Representations of Integers. IEEE Trans on Information Theory, 21(2), 194-203.
Fraenkel, A. S., & Klein, S. T. (1996). Robust universal complete codes for transmission and compression. Discrete Applied Mathematics, 64(1), 31–56. Elsevier Science Publishers B. V.